How to derive the price of WETH in terms of USDC in a Uniswap V3 pool?
What is sqrtPriceX96?
What does this number represent – 1407948368068542943726036166337703?
In Uniswap V3, the sqrtPriceX96 plays a crucial role in determining the price ratio between two tokens within a liquidity pool. Let me show you a simple explanation of how the price is calculated and how we come to the actual price from this big number above. For the purpose of the example I’ll be using the USDC/WETH pool – https://etherscan.io/address/0x88e6a0c2ddd26feeb64f039a2c41296fcb3f5640#readContract
How is the price calculated? When a pool pair is created in Uniswap V3, the two tokens are sorted by their addresses. The token with the smaller address becomes token0 and the other becomes token1. In the USDC/WETH pool, token0 is USDC and token1 is WETH. To calculate the price, Uniswap V3 uses a current exchange rate from token0 to token1. This price is the ratio of the two tokens:
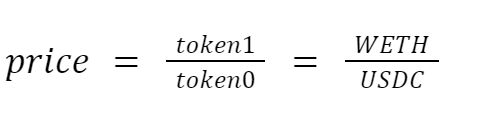
The current price is stored in the pool’s slot0 variable under sqrtPriceX96. This value represents the square root of the price ratio between the two tokens of the pool scaled by 2^96. At the time of writing, the sqrtPriceX96 for the USDC/WETH pool is:
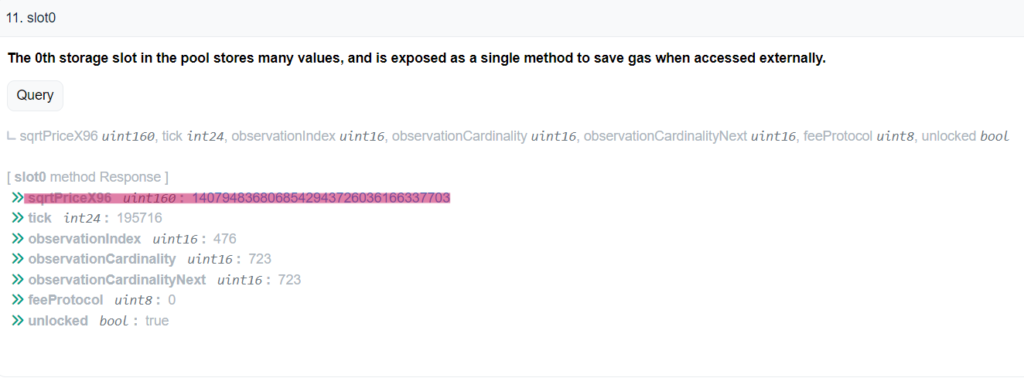
As we can observe this is a very big number and it doesn’t tell us anything special about the price. Uniswap V3 uses Q64.96 number to store the square root of the price. Q notation is a method to represent binary fixed-point numbers. The notation `Qm.n` means there are m bits for the integer part and n bits for the fractional part. In the case of sqrtPriceX96, 96 represents the fractional part (n). To remove the scaling factor we need to divide sqrtPriceX96 by 2^96. This applies to all numbers represented by Q notation – just divide by 2^n where n is the value which represents the fractional part. More for Q notation can be found here: https://en.wikipedia.org/wiki/Q_(number_format)
Let’s do some math now. First we need to divide sqrtPriceX96 by 2^96. This gives us the square root of the actual price ratio without the fractional part. To get the normalized price we need to square the result obtained in the previous step:
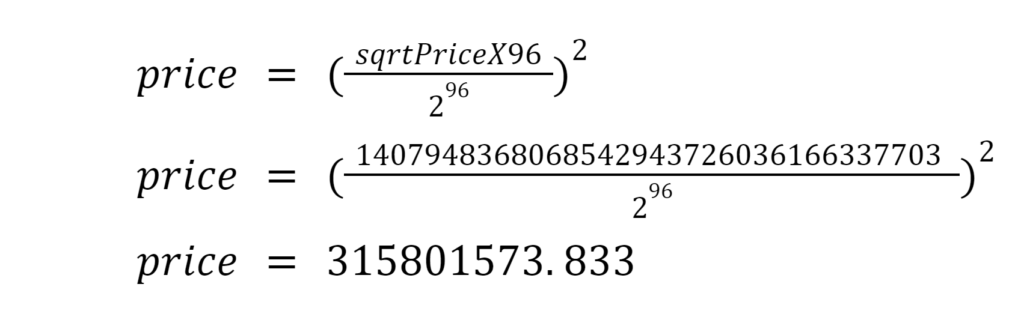
Now, since USDC and WETH tokens have different decimals (USDC has 6 decimals and WETH has 18 decimals), we need to normalize the price by adjusting for them.

And that’s it! Hmm, but this is not true, 1 WETH doesn’t cost 0.00031580157 USDC.
Actually, here we’re deriving the price of USDC in terms of WETH, meaning 1 USDC costs 0.00031580157 WETH. Remember at the beginning we sorted the tokens? As observed, Uniswap V3 saves the exchange rate between token0 and token1. To derive the price of WETH in terms of USDC we need to flip the equation (USDC/WETH). This can be done with simple math inversion:
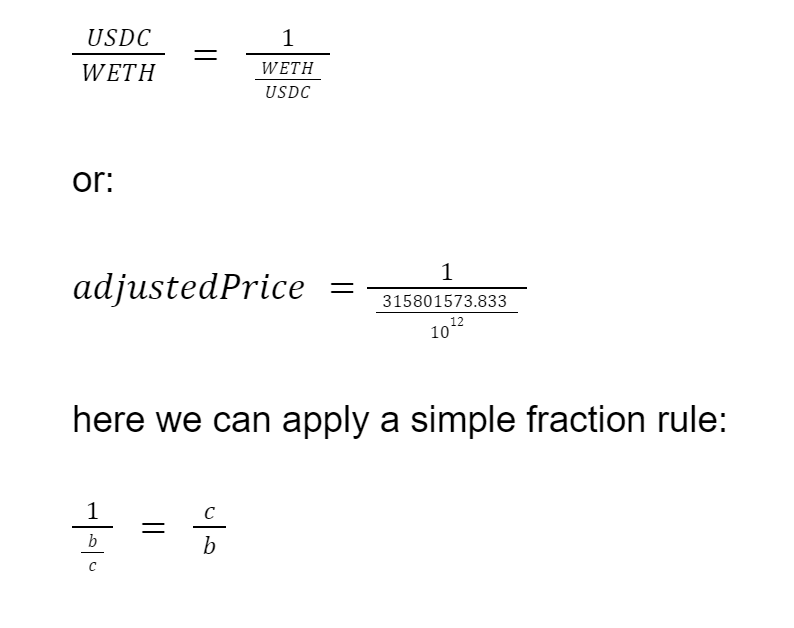
Therefore, the price of WETH in terms of USDC is approximately:
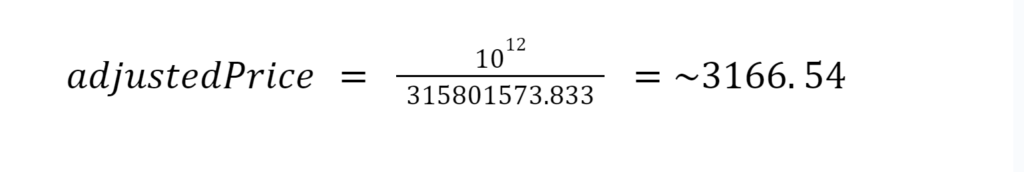
While the initial sqrtPriceX96 number might look daunting, remember, it’s simply a representation of a precise ratio used by Uniswap V3 to maintain liquidity. I hope this post helped you to better understand this topic and how the price is calculated!
Leave a Reply